模型介绍

1. 模型概述：

比例积分微分控制（proportional-integral-derivative control），简称PID控制。PID控制简单实用，应用广泛，目前大部分在车上应用的控制算法中都是PID控制。PID控制参数数量少，在对模型了解不多的情况下，通过人工反复调试参数也能得到理想的控制效果。

纵向控制说明：车辆轨迹纵向控制希望控制的是纵向的位置，但实际控制过程中横总向的位置误差通常耦合在一起，单独控制纵向位置的意义不大，因此自动驾驶车辆的纵向控制任务主要指对纵向车速的控制。

2. 文件说明：

• reference.mat 为参考轨迹数据，包含时间戳 t_ref ,x坐标 x_ref ,y坐标 y_ref 三个变量。参考轨迹通常由上游决策规划模块生成。
• Sim_Demo.slx 为Simulink文件，用于图形化编程及仿真运行。主要包括整体控制框架和被控对象模型等。
• MPC_sFunction.m 控制器s函数文件，MPC控制算法代码编写在该文件中。
• evaluator.mlx 后处理部分代码在该文件中，包括轨迹、误差、车辆状态参数曲线的绘制，动画演示。

0. 准备工作：

• 本项目可运行在MATLAB R2022a及以上版本，需安装完整的Simulink工具箱。
• 下载项目并解压，将MATLAB的工作路径设置为该文件夹；

• 或将文件夹中的文件复制到当前文件夹下。

1. 运行文件：

• 双击 Sim_Demo.slx 文件，并等待启动Simulink。
• 点击 运行 按钮开始仿真。

• 运行结束后，后在工作目录下会生成 reference_processed.mat 和 Sim_result.mat 两个数据文件。reference_processed.mat 为仿真时控制器为减少重复计算，初始化计算产生的中间数据。Sim_result.mat 为仿真结果数据。

2. 后处理运行结果：

• 仿真结束后，需要对结果进行可视化绘图。双击 evaluator.mlx 。
• 在 实时编辑器 选项卡下，按顺序点击 运行节 ，查看每一节的运行结果。

1. 仿真模型：

• 仿真模型主体包括两部分：①被控对象和②控制器。其中，控制器由s-函数编写而成，被控车辆是MATLAB提供的三自由度车辆模型，模型框图如下

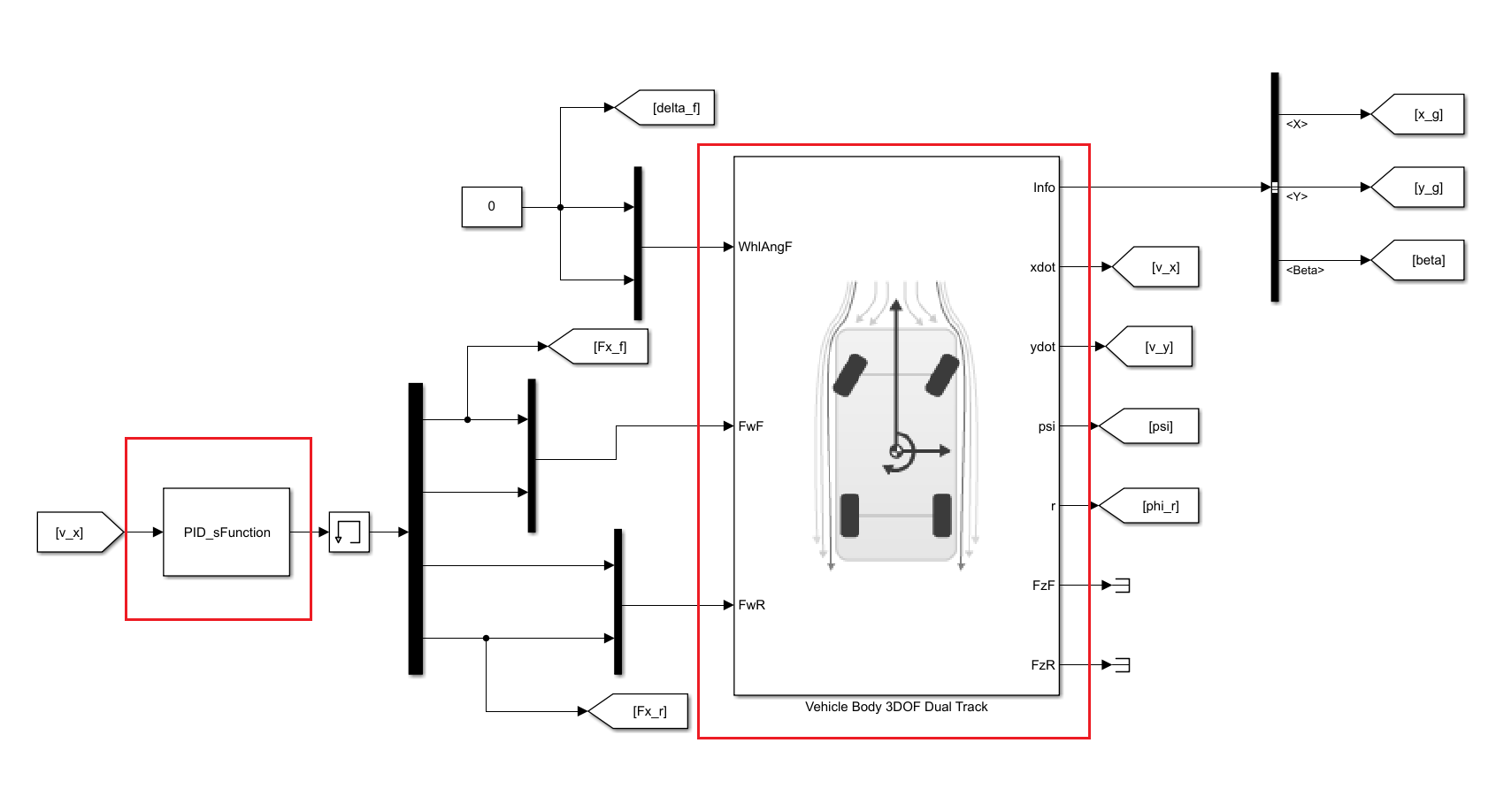
• 被控是三自由度车辆设置参数为纵向力输入

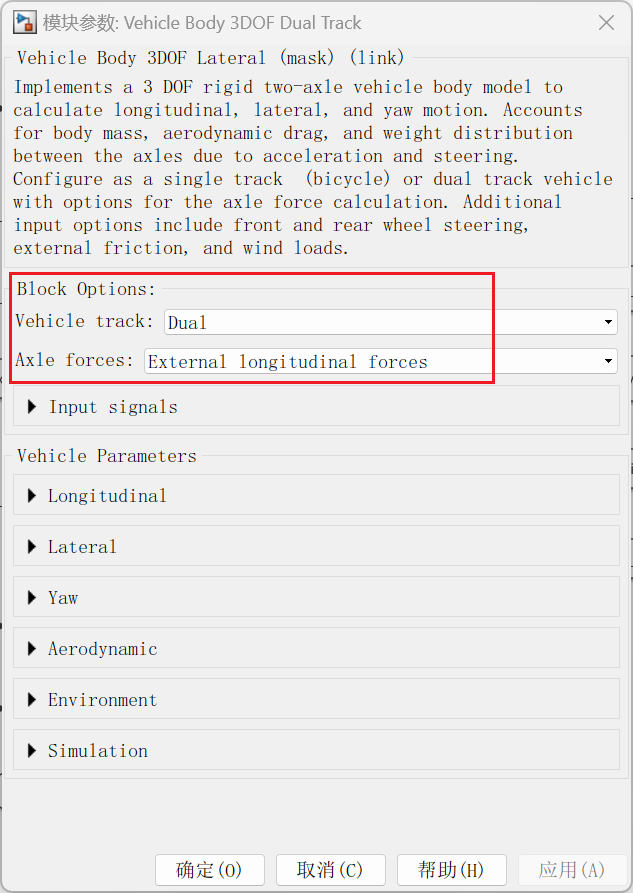
• 纵向控制时不考虑横向，即车辆跟踪直线，车辆的前轮转角始终为0

3. PID算法：

PID控制算法原理就是对误差的反馈。误差及其积分和微分的运算作为输入给到被控系统，系统只要还有误差，则PID控制器就能计算输入来纠正误差，最终让误差消失，实现控制目目标。

为统一格式，PID控制算法也用s-函数进行编写，其主函数为

• 在本案例中定义速度误差为

其中，为期望的车速，期望车速在初始函数中进行计算

• 将误差的比例，积分、微分加权后得到希望的输入加速度

其中，分别为比例、积分、微分系数

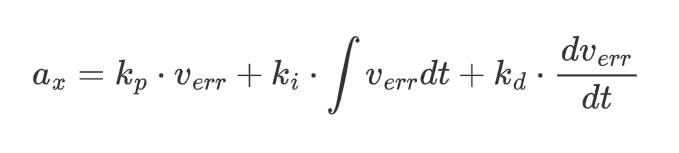
• 在s-函数中，可以用离散状态计算上述积分和微分过程

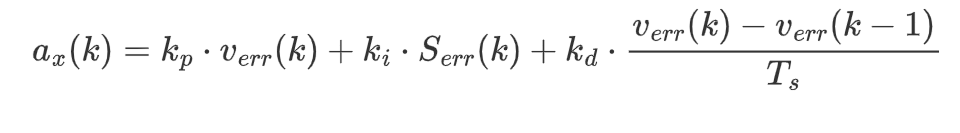
其中,为采样时间，积分用累加表示如下

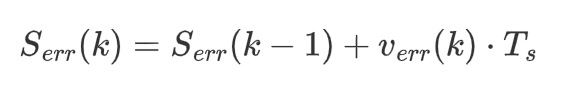
因为计算积分和微分需要用到上一时刻的变量，因此可以用到s-函数的mdlUpdate模块

3. 纵向力分配：

PID控制器得到的是纵向加速度，也可以认为是油门开度，或总的纵向力，对不同的被控车辆输入的信号需求可以是不同。对于本案例的被控对象，要求输入的是施加在四个车轮上的纵向力，为充分发挥路面的附着条件，对四个车轮上的纵向力按照垂向载荷进行简单分配。

总的纵向力为：

简单起见，可以根据静态载荷进行分配
因此前后轴的垂向力为：

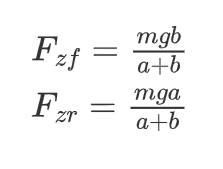
前后轴的纵向力为：

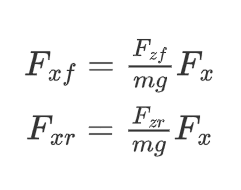
将上述过程放在s函数的输出函数中得到

4. 结果评估与可视化：

• 纵向跟踪任务指标通常简化为速度跟踪，因此指标为纵向车速跟踪控制的误差，纵向平均车速控制误差可以定义为：

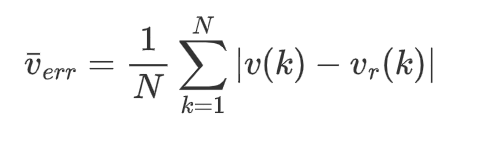
本案例中，纵向速度平均控制误差为=0.0808 m/s。

• 纵向速度跟踪曲线和误差曲线如下图

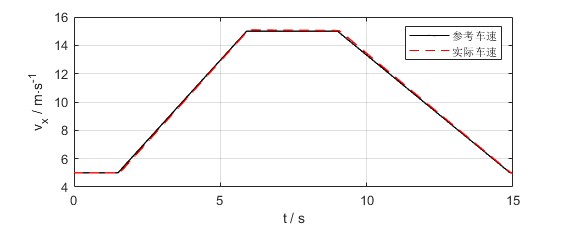
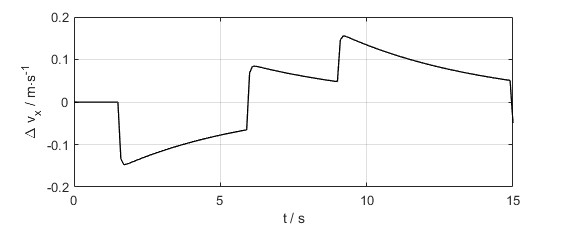
• 纵向力的输入曲线如下图

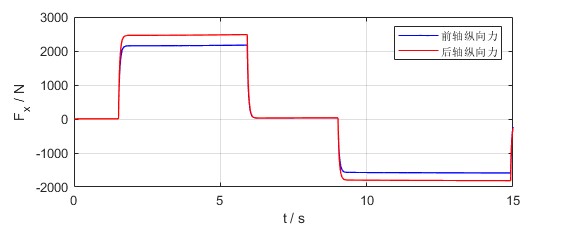
• 效果动画